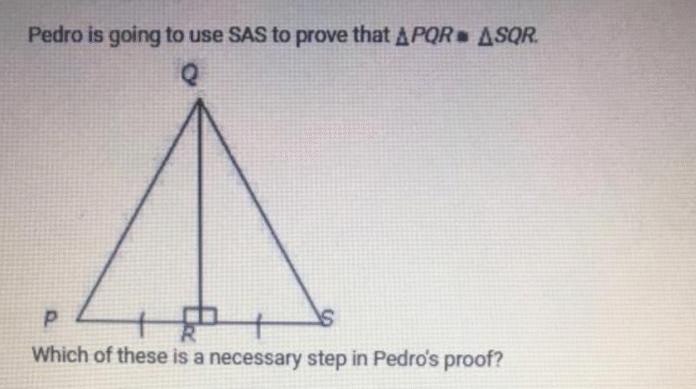
So, what’s going on here? Pedro has a triangle named PQR and he’s out to prove something pretty important: that this triangle is congruent using a geometric method called SAS. Sounds technical? Don’t worry, we’re going to break it all down in simple terms.
Why does it matter? Well, triangle congruence is one of those foundational things in geometry that pops up all over the place from designing buildings to coding computer graphics. And today, we’re focusing on a method called SAS (Side-Angle-Side) that Pedro is using to make his case.
Meet Pedro and Triangle PQR
Who Is Pedro?
Pedro is your everyday geometry student curious, logical, and maybe even a bit of a math geek. He’s been given a problem involving triangle PQR and needs to show that parts of the triangle or even the whole thing are congruent.
What Is Triangle PQR?
Triangle PQR is just a triangle named after its three vertices: P, Q, and R. Think of it as a three-cornered shape with sides connecting those points.
Why Pedro Needs to Prove Congruence
In Pedro’s geometry class, proving that triangles are congruent isn’t just a theoretical exercise it’s a skill. It’s about using logic, known measurements, and clear steps to reach a solid conclusion.
Basics of Triangle Congruence
What Does Triangle Congruence Mean?
When two triangles are congruent, they’re exactly the same in size and shape. That means all their sides and angles match up perfectly even if they’re flipped or rotated.
Real-World Applications
Believe it or not, congruent triangles are used in bridge design, GPS systems, architecture, and even art. Knowing two triangles are congruent helps ensure symmetry and stability in everything from buildings to machines.
What Is SAS (Side-Angle-Side) Congruence?
Breaking Down the SAS Rule
SAS stands for Side-Angle-Side. This rule says that if two sides and the included angle (the angle between those two sides) in one triangle are equal to the same in another triangle, the two triangles are congruent.
Why SAS Works
It’s all about rigidity. When you know two sides and the angle between them, there’s only one way to “close” the triangle. That locks it in place.
Components of SAS
One Side
Pedro starts by identifying one known side say, PQ.
The Included Angle
Next, he looks at the angle between PQ and the next side this would be ∠Q in triangle PQR.
The Second Side
Finally, he measures side QR. Now he has the two sides and the angle between them exactly what SAS requires.
Visualizing SAS in Triangle PQR
Sketching Triangle PQR
Draw a triangle. Label the corners P, Q, and R. It helps to actually see what we’re talking about.
Identifying the Given Elements
Suppose Pedro is told that PQ = 5cm, QR = 7cm, and ∠Q = 60°. That’s all he needs to apply the SAS theorem.
How Pedro Uses SAS to Prove PQR
Step-by-Step Method
-
Identify the two sides: PQ and QR
-
Identify the included angle: ∠Q
-
Check that these match the corresponding parts of another triangle
-
Conclude congruence using SAS
Finding the Necessary Measurements
Pedro might use a ruler and protractor to get accurate readings. Alternatively, he could be given the data.
Applying the SAS Rule
Once Pedro confirms the two sides and the included angle are congruent with another triangle, he states: “By SAS, triangle PQR is congruent to triangle XYZ.”
Common Mistakes and Misconceptions
Misidentifying the Included Angle
Many students mix this up. The included angle must be between the two sides not just any angle.
Using Sides Not Adjacent to the Angle
This breaks the SAS rule and could lead to wrong conclusions.
Importance of the Included Angle
Why Order Matters
SAS requires the angle to be directly between the two sides. If it’s not, you’re looking at a different theorem maybe ASA or AAS.
Comparing SAS to Other Rules
-
SSS – All three sides must match
-
ASA – Two angles and the included side
-
AAS – Two angles and any side
-
RHS – Used only for right triangles
Tools Pedro Might Use
-
Protractor – To measure angles accurately
-
Ruler – To measure the lengths of sides
-
Geometry Software – Like GeoGebra for precise constructions
Classroom Example of SAS Proof
Problem: Triangle PQR has PQ = 6 cm, QR = 8 cm, and ∠Q = 50°. Triangle XYZ has XY = 6 cm, YZ = 8 cm, and ∠Y = 50°.
Solution:
-
PQ = XY (side)
-
QR = YZ (side)
-
∠Q = ∠Y (included angle)
Therefore, by SAS, triangle PQR ≅ triangle XYZ.
Real-Life Examples of SAS Application
Architecture and Construction
Engineers use SAS principles to ensure walls, supports, and trusses are symmetrical and stable.
Engineering Designs
Machine parts often need precise shapes SAS helps in designing compatible components.
Benefits of Understanding SAS
-
Boosts logical thinking
-
Makes geometry more intuitive
-
Helps in real-world problem solving
-
Builds a foundation for higher-level math
Other Triangle Congruence Theorems Compared
SSS (Side-Side-Side)
All sides equal = congruent triangles.
ASA (Angle-Side-Angle)
Two angles and the included side.
AAS (Angle-Angle-Side)
Two angles and a non-included side.
RHS (Right-angle-Hypotenuse-Side)
Only applies to right triangles.
Final Thoughts
Pedro used logic, tools, and a good grasp of geometry to prove triangle PQR is congruent using SAS. It wasn’t magic it was methodical. By understanding rules like SAS, students can see math as a puzzle waiting to be solved, not just numbers on a board.
So, next time you’re faced with a triangle problem, channel your inner Pedro measure, analyze, and apply the right theorem.
FAQs
1. What if only two sides are equal?
Then you can’t use SAS you’d need either the included angle or a different rule like SSS.
2. Can Pedro use ASA instead of SAS?
Only if he knows two angles and the side between them. Otherwise, SAS is the better fit.
3. What does “included angle” really mean?
It’s the angle formed between the two sides you’re measuring not an outside or opposite angle.
4. Why can’t AAA prove triangle congruence?
AAA only shows shape similarity, not size. So the triangles could be same shape but different sizes.
5. Is there software that helps prove triangle congruence?
Yes! Tools like GeoGebra and Desmos are excellent for constructing and analyzing triangles.